考虑在 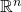 上的函数
上的函数 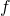 ,现在定义一个在
,现在定义一个在 ![Rendered by QuickLaTeX.com [0,2\pi]^n](https://lxsay.com/wp-content/ql-cache/quicklatex.com-ec926dee412764048b9595fea029dc5b_l3.png) 上的对应映射
上的对应映射 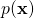 ,通过以下方式
,通过以下方式
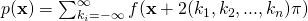
这样就可以有所根据地考虑在 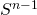 的概率测度,经过推广,也可以适用于一些简单的流形。
的概率测度,经过推广,也可以适用于一些简单的流形。
read more...
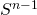 上最简单的概率测度当然是均匀分布
上最简单的概率测度当然是均匀分布 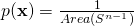
接着就是模仿正态分布的 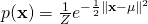 。以及使用上述映射变换正态分布的结果。利用 L2 范数就会放弃一些弯曲空间的特征,可以想象这类分布的实用性一般。用测地线长度代替也许会好一些,但仍然过于平凡。还有一些可靠的分布,需要更深入的探索。
。以及使用上述映射变换正态分布的结果。利用 L2 范数就会放弃一些弯曲空间的特征,可以想象这类分布的实用性一般。用测地线长度代替也许会好一些,但仍然过于平凡。还有一些可靠的分布,需要更深入的探索。
在流形上,滤波、平滑和贝叶斯推断可以有很强的联系,许多定义在离散空间的模型会有更舒展的表达。
![]() 上的函数
上的函数 ![]() ,现在定义一个在
,现在定义一个在 ![]() 上的对应映射
上的对应映射 ![]() ,通过以下方式
,通过以下方式![]()
![]() 的概率测度,经过推广,也可以适用于一些简单的流形。
的概率测度,经过推广,也可以适用于一些简单的流形。