LambdaRank，与星形集的上同调。
节选 <Learning to rank with Non-smooth cost functions> (CJC Burges et al., 2007)
给定查询 
与文档集，排序模型对文档集的所有文档打分，并产生长度为 
的 top- 结果（如果使用 two-stage strategy）。任何对此的重排序都是施加在其上的置换，因此这些结果关于所有重排序函数形成一个置换群。
LambdaRank 假定有隐式损失函数 
满足 
。
是搜索结果中第 
位的文档的排序分数。
显然函数 必须是在空间 
中良好定义的，应该满足：
想象在 
张成的空间中，任意 
都是定义在此空间的函数，于是上式是指 函数沿此空间内给定两点间的任意路径积分都能“还原”到损失函数 。满足这样性质的空间称为“星形集” (star-shaped set)，这样的集合中存在一点，使得集合内所有点与该点的线段都属于该集合。进一步又有，
(1) 
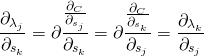
中间的等号成立是因为交换微分顺序不改变结果。所以关于所有 
函数 的 Jacobian 矩阵是对称的。如果损失函数 是凸的，那么 关于 的 Hessian 矩阵就是对称正定阵，自动满足以上条件。希望损失函数是凸函数的原因是因为这样可以使用梯度下降法找到最优解（……………..）
现在用微分拓扑的角度，考虑在空间 中的向量 
，定义 1-形式 
。
可以看作是一个“有向的”微元。 LambdaRank 的假定可以写成 
，
是外微分。想要找到满足假定的一般的 不容易，但是庞加莱引理 (Poincare’s lemma) 给出一个结论：在星形集中，
当且仅当 （每个闭形式都是恰当形式）。因此现在只需要寻找满足 的 函数，具体来说，就是寻找合适的每个分量 。而这个条件，就等价于上面的 “Jacobian 条件”。