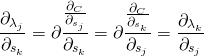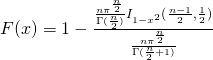大蛇薙

Posted on 2020-05-012020-05-01 by chiccs

“流形检索”提要。

最近，我写的一篇文章进了 SIGIR 2020 这个会。它很短，对我来说是一个“锚”，这样以后写作的时候起码有资料可以引用，不用像民科一样没有根据地长篇大论。

这篇文章只想讲一件事：在连续的集合上可以定义“语言”。如此，所谓的“神经排序”就是连续点集上的统计语言模型，因此所谓的“end-to-end” 就是内蕴的性质。“结构”(structure)与“测度”(measure)是“新语义检索”的基础，它们分别概括了“表示法”(representation)和“模型”(retrieval model)这两个传统的概念。它必须收敛，收敛性是模型正确性和性能的一种估计。有些公司的什么“技术博客”总喜欢吹嘘“数据决定模型性能”这类有机械唯物主义意味的观点，奉之为“指导思想”，把自己的命运完全交给收集用户偶然的行为（这些用户行得通，那些用户呢？当然可以说自己的模型都能奏效，但这就不只是数据的问题），还有对 learning-to-rank 望文生义的涂改，不想多说，专心做生意吧。

流形上的概率论很早就有了，这与信息几何(information geometry)的发展有关，只是它们研究的大多都是参数空间的分布，本文反而考虑变量空间的事情。以前那些形如“xx learning/clustering on manifold”的文章，为了让梯度可以直接在曲面上更新，一定会用指数映射之类的方法。这些画蛇添足的内容我全都放弃了。从某种意义上说，直接更新梯度之后再把向量归一化再算测度，是一种“传输”，这暗示了那些 xx norm 之类的方法真正的含义。还有一些譬如 ngram 表示之类的问题，可以在复流形上解决，也可以用一些像向量一样的东西代替。

其实，这也和量子检索(quantum retrieval)有关，只是前面的人比较极端，试图用量子力学直接概括整个领域。

这篇论文的写作和发表可能得到了无法知晓的支持，在此顺带以真诚致谢。我从不打算靠做此类研究谋生。这个时代，智力正常的人都应该想出一百种赚钱的方式，在每个行业只要花足够多的时间和毅力，最后都能得到可观的财富，做到底就知道这其实是国家实力发展的结果。在一个动荡的社会里很难静下心来做事，这是我暂时离开香港的原因，无法一直在负面的情绪中工作和生活，这会扭曲人的心灵，神智将和社会一样撕裂。但我会认为，这篇论文是给香港社会的答谢，尽管它没有了不起的内容，我也只是很渺小的一个人，能够没有负担地走出去。

这是“拳皇”系列博文的结束，台湾知名格斗游戏选手“Nikolai 保力達”的视频给了我很多的乐趣，过段时间再写下个系列。

鬼烧

Posted on 2019-11-092019-11-09 by chiccs

所谓“策略随机检索” (Strategic Random Retrieval)

本来，在这个系列的最后，我准备放上几个 runs，进行期待已久的“清算”。可是有个小朋友给我分享了自己好友在父母长达十余年外遇、家暴的历史下艰难生活的故事，告诉我要“be kind to others”。所以那种“灭门”的事情以后再说。现在想写关于 diversity 的故事。

这个世界充满了优胜劣汰，所有设计模型的人都想着如何 do the best estimation given observations. 供给信息的人则想着如何 maximize the importance of their features. 所以系统忙着 learning to rank，供给者忙着做 SEO，而用户则忙着辨认真切的结果和“充值”的结果。这个三方系统的内部成本在这样的内耗中不断增加。正确性和相关性、以及任何试图学习这两者的性质，最后都失去意义。

一种没有排序的检索从随机返回任何结果中产生。为了满足愉悦和可靠的目标，在最开始它可以从向传统的检索施加有策略的扰动开始。这种扰动可以是一种约束，也可以是一种行为。

**（当然我说的不是“转化率”。敢把转化率当成吹嘘的资本写进每次署名七八个作者的的学术论文里面也就只有国内几个胆子大的公司才能成就如此伟业。）

七十五式改

Posted on 2019-09-142019-09-14 by chiccs

A toy retrieval model (H-RM0).

查询 $Q=q_1 q_2 .. q_n$ ，文档 $D=t_1 t_2 ... t_m$ 。假定 $S^{N-1}$ 上有 $n$ 个初始点各自符合分布 $\mathcal{N}(\mu_i , \sigma_i)$ ，还有 $m$ 个点表示文档词的位置。
选取 $S^{N-1}$ 上任意一个度规。对每个初始点和文档点，计算距离 $M_{ij}$ 。把 $M_{ij}$ 作为分布的变量，计算分数 $p_{ij}$ 。
对每个初始点 $i$ 使用“路径选择器” $M_{p}^{i}(p_{i1},p_{i2}, ... , p_{im})$
返回 $\sum {log M_{p}^{i}}$

这其实是什么呢，去掉了 learning to rank 层，并且相差一个输入线性变换的 K-NRM (Xiong et al., 2017)。K-NRM 对 “每一行” 都使用 $K$ 个核函数。如果设计得当， $K$ 也可以是内生变量。

本系列 posts 只用一些简单的概念讨论检索的输入和表示，还有两篇结束。下个系列使用几何工具进行信号的变换，它们对应一部分“隐层”的行为。

轹铁

Posted on 2019-08-152019-08-16 by chiccs

LambdaRank，与星形集的上同调。

节选 <Learning to rank with Non-smooth cost functions> (CJC Burges et al., 2007)

给定查询 $Q$ 与文档集，排序模型对文档集的所有文档打分，并产生长度为 $n$ 的 top- $n$ 结果（如果使用 two-stage strategy）。任何对此的重排序都是施加在其上的置换，因此这些结果关于所有重排序函数形成一个置换群。

LambdaRank 假定有隐式损失函数 $C$ 满足 $\frac{\partial_C }{\partial_{s_j}}=-\lambda_{j}(s_1,l_1,...,s_{n_i},l_{n_i})$ 。 $s_j$ 是搜索结果中第 $j$ 位的文档的排序分数。

显然函数 $C$ 必须是在空间 $(s_1,l_1,...,s_{n_i},l_{n_i})$ 中良好定义的，应该满足： $C=\int \lambda_{j} d_{s_j}, \forall j \in {1..n_i}$

想象在 $(s_1,...,s_{n_i})$ 张成的空间中，任意 $\lambda$ 都是定义在此空间的函数，于是上式是指 $\lambda$ 函数沿此空间内给定两点间的任意路径积分都能“还原”到损失函数 $C$ 。满足这样性质的空间称为“星形集” (star-shaped set)，这样的集合中存在一点，使得集合内所有点与该点的线段都属于该集合。进一步又有，

(1) $\begin{equation*} \frac{\partial_{\lambda_j} }{\partial_{s_k}} =\partial \frac{\frac{\partial_C }{\partial_{s_j}}}{\partial_{s_k}}=\partial \frac{\frac{\partial_C }{\partial_{s_k}}}{\partial_{s_j}}=\frac{\partial_{\lambda_k} }{\partial_{s_j}} \end{equation*}$

中间的等号成立是因为交换微分顺序不改变结果。所以关于所有 $\lambda_j$ 函数的 Jacobian 矩阵是对称的。如果损失函数 $C$ 是凸的，那么 $C$ 关于 $(s_1,...,s_{n_i})$ 的 Hessian 矩阵就是对称正定阵，自动满足以上条件。希望损失函数是凸函数的原因是因为这样可以使用梯度下降法找到最优解（……………..）

现在用微分拓扑的角度，考虑在空间 $(s_1,...,s_{n_i})$ 中的向量 $(\lambda_1,...,\lambda_{n_i})$ ，定义 1-形式 $\lambda=\sum \lambda_j d_{s_j}$ 。 $d_{s_j}$ 可以看作是一个“有向的”微元。 LambdaRank 的假定可以写成 $\lambda=dC$ ， $d$ 是外微分。想要找到满足假定的一般的 $\lambda$ 不容易，但是庞加莱引理 (Poincare’s lemma) 给出一个结论：在星形集中， $d\lambda=0$ 当且仅当 $\lambda=dC$ （每个闭形式都是恰当形式）。因此现在只需要寻找满足 $d\lambda=0$ 的 $\lambda$ 函数，具体来说，就是寻找合适的每个分量 $\lambda_j$ 。而这个条件，就等价于上面的 “Jacobian 条件”。

罪咏

Posted on 2019-07-152019-07-15 by chiccs

最近信息检索社群的研究动向之一是所谓交互式检索的方法论（interactive/conversational/online + retrieval/learning to rank/blahblahblah.. ）。简单来说，就是从用户的角度来考虑检索问题，因此系统的设计和评价方式需要从用户的实际行为和反馈出发，而不是通过假设单方面推进检索的过程。

以唯物史观看待（强调这点是因为，也可以有不同的角度认为这是某几个“大佬”以个人意志带动的潮流。），这种研究兴趣的迁移是对当前自然语言处理研究的被动回应和规避：传统的信息检索研究大多和 NLP 研究一样，是在离线的数据集上评价模型。由于神经网络强大的学习能力，以及信息检索和自然语言处理的相关性，现在信息检索确实有被自然语言处理的研究狂潮淹没的隐忧或危机。IR 社群亟需重新发掘信息检索的特异性，以示区别。因此交互性作为搜索引擎最显著的特征之一便被提上日程。
交互性检索是对多个已有方向的自然扩展。以信息供给（information supply）的角度，离线数据集的标注成本实在惊人并且存在道德风险，而用户行为数据丰富而有趣。通过学习用户行为再服务用户再收集数据，产生的“乘数效应”显然是比通过学习少数标注数据再服务用户的方法要大得多。另外，这也是 “searching as learning” 观点的延伸，只是强监督信号变成了弱监督信号。
现在的信息检索研究缺乏强有力的数学基础：许多最近的研究的表述方式，除了用结果说话的“炼金术”以外，就是一些高中级别的概率统计知识加上一点微积分，再加上作者自己想象的故事，最后再添上用海量实验结果堆砌的所谓“实验分析”。如果这一点不被解决，我不觉得能有什么很重要的进展。

奈落落

Posted on 2019-05-312019-06-01 by chiccs

这一篇不讲武功，只讲想法。

前几天看了一篇 NIPS 2017 的文章<Deep Hyperspherical Learning>。很显然，作者也想到了 $S^{n-1}$ 上的内积和测地线的性质。看到这篇文章的第二节的前两段的时候，我觉得自己不用再写这些东西，直接抱大腿、用现成的模型就行。但作者紧接着只是介绍自己提出的 SphereConv 这个卷积层。

（这个作者在 NIPS 2018 又有一篇文章 <Learning towards Minimum Hyperspherical Energy>。作者又想了一个电子分布能量的概念，其实就是类比电场的多体问题的稳态解。然而这种东西只是一种根据问题的语义自定义的场而不是空间本身的性质。）

很多从无到有的事情还是要自己做。

很多 word embedding 模型在训练的时候都做这样的事情：首先给每个词指定一个随机向量，然后根据总体损失函数的向量场更新词向量。如果用 word as point 的观点，这就是说词代表的点在一个 n 维流形做有限次的跃迁。

另一方面，假定这些 word embedding 模型是收敛的。原则上说，对于任意的初始值，词向量在训练后都能保持内积，也就是说对于任意的两个词向量它们的内积是不变的。其次，对于不同的初值，词的向量表示很有可能也是不同的。这是由于词汇空间和流形不等势造成的稀疏性。对一个给定的初值向量的某些分量施加一个无穷小的微扰，得到的结果应该是相同的。因此这暗示：

n 维流形上的每个点都对应一个词汇空间的元素。

紧接着做出连续性假设：

每个词汇空间的元素在 n 维流形上对应的点集都是连续的，或是不相交连续点集的并。

这就是说：

每个词在 n 维流形上都具有非零 (Lebesgue) 测度。

超重当

Posted on 2019-05-222019-05-23 by chiccs

有了“测地线”的概念，就可以在 $S^{n-1}$ 上解释一些模型的行为，比如位置语言模型 (Positional Language Model)。

现在，PLM 的假设 “a term at each position can propagate its occurrence at that position to other positions within the same document through a proximity-based density function” (Lv and Zhai, 2009) 是内蕴的。一个词对应 $S^{n-1}$ 上的一个点，沿着测地线到达另一个点，产生语素变换的损失。所谓的 “virtual document” 就是在指定距离处的有限点集。用“word as a point”这个强假设，代替原文中有点勉强的假设，还是比较划算的，因为可以定义内积和距离。
proximity-based kernel function for propagation 是关于路径的损失密度函数。也许可以写成路径积分，也许不是测地线。反正就是类似的意思。

一些查询扩展(query expansion)的方法也可以用这个套路解释，但意义不大。PLM 还是基于词的多项分布，用的是计数测度，所以当时来看，结果没有提高很多，很正常。

所以接下来，就是利用 $S^{n-1}$ 的性质得到更好的估计。过段时间再写。

扇沟流

Posted on 2019-05-142019-05-16 by chiccs

有很多的检索模型，都使用这样的策略：首先使用一种简单的检索模型（比如 LM, BM25 和 TF-IDF）找出最接近 query 的前 N 个结果（比如 top 100/500/1000），然后再使用自己的模型重新对这些结果打分并排序(rerank)。

这些模型可以分成两类：对 N 不敏感的和对 N 敏感的。

随着 N 的增大，对 N 不敏感的模型的性能整体上只会在一个很小的区间内波动，这称为它们具有“收敛性”。对 N 敏感的模型的性能一般和 N 的取值是负相关的，也许 N=100 的时候性能很好，但是当 N 增大数倍之后结果就变得惨不忍睹。

为什么会有这种区别呢？这只取决于这些模型是否是词汇空间上良好定义的测度。正确的测度会因为大数定律的限制而变得稳定，不标准的度量会因为有偏的估计而失常。Batch normalization 为什么有用呢？也许其实和什么“独立同分布假设”之类关系不大，只是为一堆杂乱无章的东西(batch)强行定义了一个良好的概率测度(normalization)。

所以想要检验没有理论基础的模型，最好不要用 two-stage strategy，而要浪费大把时间直接 rank the whole collection。不然文章发出来，最多也只是有人引用、没人敢用。

琴月

Posted on 2019-05-082019-05-08 by chiccs

$V$ 在 $S^{n-1}$ 均匀分布， $U$ 是其上的固定点， $U \cdot V \sim ?$

定义累积分布 $F(X)=Pr(U \cdot V < x)$
以 $U$ 的正方向为轴，想象用一个垂直于 $U$ 并与其它 $n-1$ 个坐标轴平行的超平面，将 $S^{n-1}$ 截成两个部分
满足条件的点集构成 $S^{n-1}$ 上非球缺的部分

$F(x)=1-\frac{\frac{n\pi^{\frac{n}{2}}}{\Gamma(\frac{n}{2})}I_{1-x^2}(\frac{n-1}{2},\frac{1}{2})}{\frac{n\pi^{\frac{n}{2}}}{\Gamma(\frac{n}{2}+1)}}$

$I$ 是正则化不完全 Beta 函数

$I_{1-x^2}(\frac{n-1}{2},\frac{1}{2})=\frac{\int_{0}^{1-x^2}t^{\frac{n-3}{2}}(1-t)^{-0.5}}{\int_{0}^{1}t^{\frac{n-3}{2}}(1-t)^{-0.5}}$

$f(x)\propto (1-x^2)^{\frac{n-3}{2}}$

简单修改 $V$ 的分布条件，结论对 $S^{n-1}$ 上的任意分布几乎成立。从某种意义上说，所有使用 word embedding 而不考虑维度影响的 NLP/IR 模型都是有问题的。

开始名为新·语义检索的转向。

TREC CAR 2018 随想

Posted on 2018-12-042018-12-04 by chiccs

结果如何？直接看图吧。

今年春节的时候就想开发一个比去年更好的方法。一直被阻拦，只能断断续续地做实验。在 cikm 交稿之后，离 trec 的 deadline 只剩一两周的时候匆忙继续。发现了 Wikipedia article information 可以增强性能。总算有东西可以提交。

这个 task 有几个比较奇特的地方：

一是输入输出格式比较复杂，要自己用 trec-car-tools 从 cbor 里面读取每个 query path。这两年还有区分 query 的类型，比如 outlines（文章标题）, hierarchical（最具体的章节路径）。输出的时候要加上 “enwiki:” 或者 “tqa”这样的前缀。说实话不能理解为什么要这么折腾。

二是这个任务的 evaluation 其实是有偏差的 (biased)。评估方式分三种 Automatic, manual 和 lenient。Automatic 就是用维基百科的章节路径当作 query，然后章节里面包含的段落当作 ground truth。 manual 和 lenient 是按照 trec 标准的人工评测。个人发现 SDM 类的模型经过充分的调参以后可以在 automatic 上取得 state-of-the-art 的结果，但是 manual 和 lenient 的评测结果和其他方法比就还有差距。这其实反映了统计语言模型和 neural ranking model 对 concept salience 的假设是不一样的。

三是我这次用 Wikipedia article 的信息作为一个特征输入，由于程序的一个 bug，这个部分全部输出为0，结果竟然还比没有集成这个特征的原始模型提升了至少 15%。这起码说明能找到对应 Wikipedia article 的段落更有可能成为答案。我感觉 Laura 可能已经发现了这个问题，后续的数据集应该会变得更加 Wikipedia-free。

反正结果就是这样，这次其他的队伍用了很多成熟的 learning to rank 的方法，再加上一些 hand-crafted feature 和 query expansion mechnism（比如 RM3。。。）。取得好的结果是意料之中。恭喜。

我十月份申请的美签居然还在 administrative processing! 最后没去参加 trec。只好给 Laura 发邮件解释原因，给 hilton 发邮件取消房间，交 no-show charge，取消机票。我很讨厌处理这种琐事，这次耗尽了所有精力。 us visa office seems to believe that the higher education a Chinese get, the more dangerous is he or she to the United States. This is truly ridiculous and racist. 另外美国香港领事馆是我见过的服务态度最恶劣的领事馆，只能说人在做天在看。非常失望，这辈子都不考虑去美国。

总的来说今年的这件事算是彻底的失败了。但这不是我的失败，也不是我的耻辱。我只是在有限的时间里做了自己能做的所有事情。有些阻碍不是我能跨越的，有些装睡的人不是我能叫醒的。如果一百年以后的哪天我死了，我的墓碑上也许会有一句话：此人此生光明磊落。

chiccs's Blog

Time is Scarce, Life is Short

Tag: Information Retrieval

大蛇薙

鬼烧

七十五式改

轹铁

罪咏

奈落落

超重当

扇沟流

琴月

TREC CAR 2018 随想